Creating high-quality training data is a critical step when designing algorithms to detect and classify cells. Training data are example data points that are used to develop an algorithm. For example: a set of images, each of which might or might not contain a cell, plus human-generated tags indicating whether each image actually contains a cell. These data usually have to be labeled by a person; the algorithms are then trained to reproduce and generalize the human-generated labels. Algorithms can only be as accurate as the data which are used for training. Care should be taken, then, to optimize the accuracy of training data.
One key strategy to generate accurate training labels is to have each candidate cell be labeled by more than one person; the cell then gets the label assigned by the maximum number of people. To illustrate the usefulness of this approach, consider a hypothetical dataset in which 50% of the training data points are positive (i.e. contain a cell), and 50% are negative (i.e. do not contain a cell). Let’s assume that the people labeling the training data are pretty good, but not perfect – they get 90% of the points right, on average. How does adding more people affect the quality of the dataset?
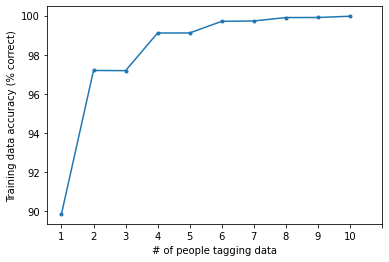
As might be expected, accuracy increases as the number of people increases. But 2 people seems hardly an improvement over one person, whereas 3 people is a huge jump up, cutting the error by more than half. Why is that?
To unpack this, consider the two-vote case. What happens for the candidates where one person says it is a cell and the other person says that it isn’t? Both people are assumed to have similar accuracy, so neither is more likely to be correct than the other. Furthermore, positives and negatives are equally likely, so we can’t get any hints from the distribution of the data either. This means that, in any case where the labels are different, having two people still doesn’t give us enough information to label these cells.
However, as soon as a third person is added, we now have a lot more information: for every candidate cell, there are three votes, meaning that all ties have been broken. Our confidence about each cell’s label is thus much higher than before, leading to a large jump in accuracy.
Interestingly, this “tiebreaker” effect should be less prominent in skewed datasets. Consider an extreme dataset, where 90% of the candidates are not really cells, and only 10% are truly cells. If two people label a given image differently, we can make an educated guess based on the fact that negative examples are a lot more common in the dataset: when in doubt, always guess that a candidate is negative. In the image below, you can see how accuracy scales with number of people tagging the data, for datasets with different underlying distributions:
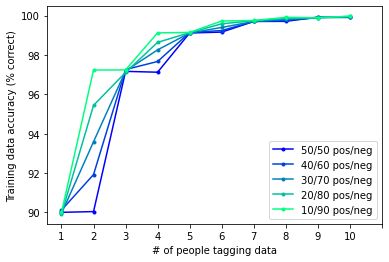
You can see that the added value of a third person decreases depending on how skewed the dataset is: a tiebreaker is less important when you can make strong assumptions about the underlying positive rate.
Of course, keep in mind that this is using a simplified set of assumptions – for example, in real life, some cells will be more difficult to classify than others, meaning that the likelihood of getting a wrong answer should be correlated between users.
When labeling training data, then, keep in mind two things: first, adding a person to act as a tiebreaker can generate a large jump in your accuracy. It is also important to keep in mind the expected percentage of positive cells in your training data; the advantage of having a tiebreaking vote is strongest in a balanced dataset.
Of course, if you would rather skip over laboriously generating training data and optimizing classification algorithms, you could instead use LifeCanvas’ 3D analysis software, SmartAnalytics. With models customized to identify cells in 3D histological data, plus brain atlas registration and automated generation of publication-quality summary plots, SmartAnalytics takes you seamlessly from image to quantification.
Want to check the math for yourself? The exercise basically boils down to an application of Bayes’ rule:
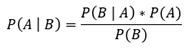
In this case I’m modeling each person’s probability of labeling a positive/negative as independent of each other person, and assuming that false positives and false negatives occur at the same rate.

